Most arcs in a Petri net within SNAKES are annotated with values, expressions or variables. However, other types of annotations are available. This post reviews all the types of arc annotations available in SNAKES.

To illustrate the various arc annotations, we will use a simple net pattern generated with the following factory function that creates a net with one transition to consume cons from an input place src and produce prod to an output place tgt.

import snakes.plugins
snakes.plugins.load("gv", "snakes.nets", "nets")
from nets import *

def factory (cons, prod, init=[1, 2, 3]) :
    n = PetriNet("N")
    n.add_place(Place("src", init))
    n.add_place(Place("tgt", []))
    t = Transition("t")
    n.add_transition(t)
    n.add_input("src", "t", cons)
    n.add_output("tgt", "t", prod)
    return n, t, t.modes()

This function returns the net as well as the Transition object and its modes.

Values, variables and expressions

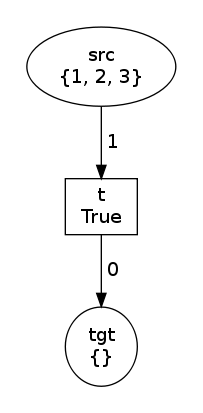
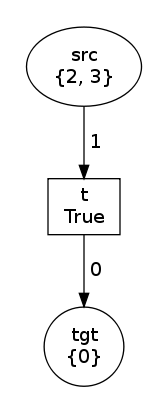
Let's start with the most basic annotation: an instance of Value allows to consume or produce a known Python value. For instance we consume 1 and produce 0:

net, trans, modes = factory(Value(1), Value(0))
net.draw("value-0.png")
print modes
trans.fire(modes[0])
net.draw("value-1.png")

In this case, modes=[Substitution()] and the two states of the net are:

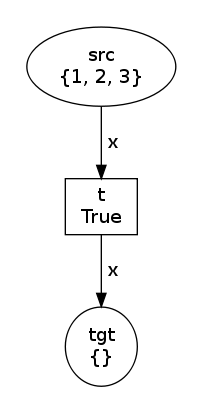
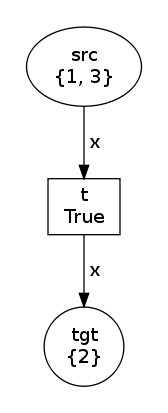
If now we use a variable instead of the values:

net, trans, modes = factory(Variable("x"), Variable("x"))
net.draw("variable-0.png")
print modes
trans.fire(modes[1])
net.draw("variable-1.png")

Then, we have modes=[Substitution(x=1), Substitution(x=2), Substitution(x=3)] and the two states are:

Remark: method modes returns a list whose order is arbitrary and may vary depending on your Python version of implementation. So, the example above and those below may be executed slightly differently on your installation.

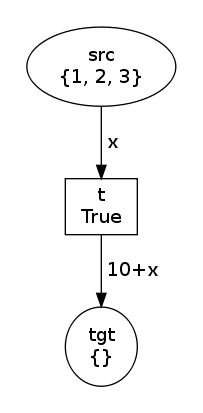
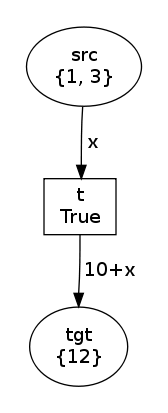
Using an Expression instance is possible only for the output arcs (explanation here). So we may specify:

net, trans, modes = factory(Variable("x"), Expression("10+x"))
net.draw("expression-0.png")
print modes
trans.fire(modes[1])
net.draw("expression-1.png")

In this case, modes is the same but the produced value has changed:

Multiple tokens

Several tokens may be consumed or produced with the same arc using a MutiArc annotation. For instance:

net, trans, modes = factory(
    MultiArc([Variable("x"), Variable("y")]),
    MultiArc([Expression("x+y"), Value(0), Expression("x<y")])
)
net.draw("multiarc-0.png")
print modes
trans.fire(modes[1])
net.draw("multiarc-1.png")

In this example, both arcs are annotated with a MultiArc:

• the input arc consumes two values that are bound to variables x and y thanks to the two Variable instances;
• the output arc produces three values, two of which being computed with an Expression instance, the third one being value 0.

The constructor of MultiArc expects a list (or any iterable) of others arc annotations, each should be allowed on the arc. For instance, we could not use an Expression instance in the components of the input multi-arc because expressions are not allowed on input arcs.

The printed modes here are [Substitution(y=2, x=1), Substitution(y=3, x=1), Substitution(y=1, x=2), Substitution(y=3, x=2), Substitution(y=1, x=3), Substitution(y=2, x=3)] so that we get the two states:

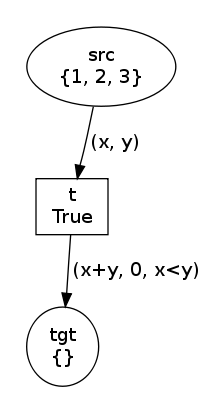
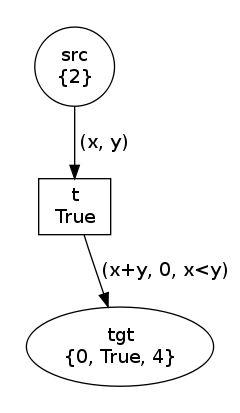
Structured tokens

Instances of class Tuple allow to match tokens that are themselves Python tuples. For instance, let's initialise our input place with pairs of integers:

net, trans, modes = factory(
    Tuple([Variable("x"), Variable("y")]),
    Tuple([Expression("x+y"), Value(0), Expression("x<y")]),
    [(0,1), (1,2), (2,3)]
)
net.draw("tuple-0.png")
print modes
trans.fire(modes[1])
net.draw("tuple-1.png")

Now, we have modes=[Substitution(y=1, x=0), Substitution(y=2, x=1), Substitution(y=3, x=2)] and the two states are:

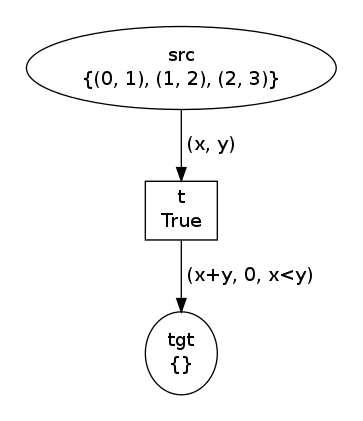
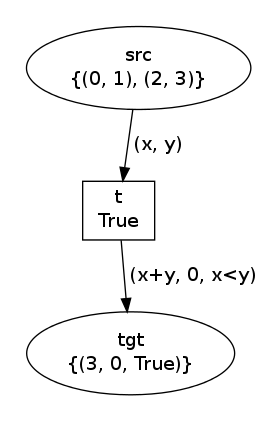
Notice that instances of Tuple may be nested arbitrarily. The only restriction is like for MultiArc that no Expression may appear on an input arc, even hidden in a nest of Tuple instances.

Flush and test arcs

Two other classes of annotations are available in SNAKES, which are actually extensions of Petri nets. The first class is Flush that, used on an input arc, allows to consume the whole marking of a place and bind it to a variable. Consider the following example:

net, trans, modes = factory(Flush("x"), Variable("x"))
net.draw("flush-0.png")
print modes
trans.fire(modes[0])
net.draw("flush-1.png")

Now, we have modes=[Substitution(x=MultiSet([1, 2, 3]))] which shows that the effect of Flush("x") on an input arc is to bind x to the multiset of tokens held by input arcs. The two states are now:

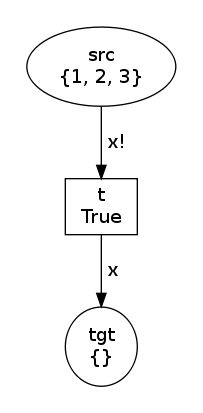
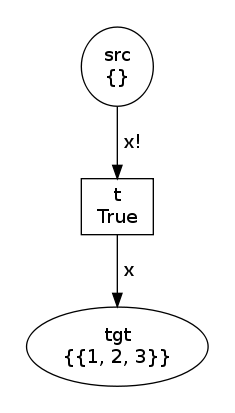
Notice in the second state that place tgt contains exactly one token that is actually a MultiSet object. Notice also that if in the second state we execute trans.modes(), we get [Substitution(x=MultiSet([]))] and not an empty list: a flush input arc never forbids execution, which allows to implement a zero test.

Flush arcs may be used on output arcs, in which case they would be better called fill arcs: the constructor expects a Python expression whose evaluation yields an object that is iterated over in order to produce a collection of tokens in the output place. For instance:

net, trans, modes = factory(Flush("x"), Flush("x*2"))
net.draw("flushes-0.png")
print modes
trans.fire(modes[0])
net.draw("flushes-1.png")

The first state and the modes are the same but the second state differs:

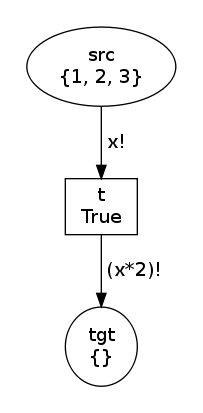
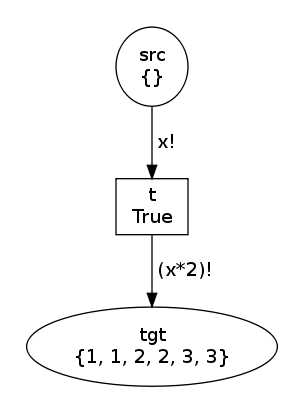
Indeed, the output flush arc evaluates x*2 that is MultiSet([1, 2, 3])*2 that yields MultiSet([1, 1, 2, 2, 3, 3]). Then, each item in this new multiset is added as a token in the output place.

Finally, class Test allows to encapsulate another annotation (any that would be allowed) and behaves exactly the same except that it actually does not consume or produce tokens. Used on an input arc, it allows to implement a read arc; used on an output arc, it allows to test whether the tokens would be accepted or not by the place type. For instance, let's modify our third example with Expression:

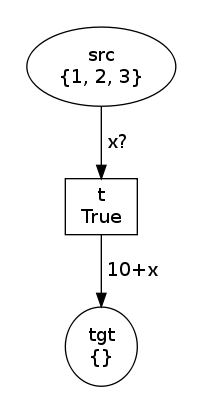
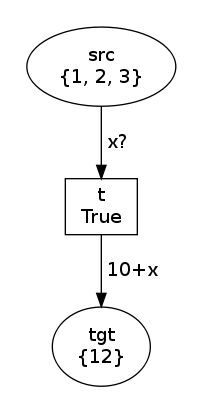
net, trans, modes = factory(Test(Variable("x")), Expression("10+x"))
net.draw("test-0.png")
print modes
trans.fire(modes[1])
net.draw("test-1.png")

The modes are exactly the same [Substitution(x=1), Substitution(x=2), Substitution(x=3)] but now, in the second state, the marking in the input place has not been modified: