Getting SNAKES and installing it

The preferred method to install SNAKES is to use pip install SNAKES, you will get the latest release from the Python Package Index. If you want the very last version directly from the git repository, use pip install git+git://github.com/fpom/snakes instead.

Optionally, you may want to install GraphViz to be able to draw nets. Doing so, take care that executable dot (or dot.exe under Windows) must be in your PATH environment variable otherwise SNAKES will be unable to invoke it. Note that installing GraphViz is required if you want to use ABCD or plugin gv (to draw Petri nets).

To install SNAKES from source, first download the latest version from SNAKES' GitHub page. Either clone the repository or download and uncompress the ZIP archive, then run python setup.py install at the command line. But note that this will do exactly the same as pip install git+git://github.com/fpom/snakes.

SNAKES should work with any Python version starting from 2.5 (including 3.x), but it will not work for an older version.

Creating nets and firing transitions

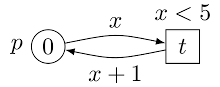Let's define a simple coloured Petri net and see how to fire transitions and get markings. This net has a single transition that increments an integer valued token (so, 0 is the value of the token, not a number of tokens) held by a single place, the incrementation stops when the value is 5 thanks to a guard on the transition. To define this net, we must load SNAKES, define a Petri net (lets call it 'First net'), add the place (called 'p'), add the transition (called 't') and then connect them with arcs.

Remark: most code snippets below are copied from an interactive Python shell, but they could equally be executed in a script. Use buttons >>> at the top-right to toggle shell prompt/output.

>>> from snakes.nets import *
>>> n = PetriNet('First net')
>>> n.add_place(Place('p', [0]))
>>> n.add_transition(Transition('t', Expression('x<5')))
>>> n.add_input('p', 't', Variable('x'))
>>> n.add_output('p', 't', Expression('x+1'))

Expression Place('p', [0]) constructs a new instance of class Place that expects the name of the place as its first argument. The second argument is optional and is the initial marking of the place, that can be given as a list tokens (or any iterable collection).

In order to build the transition, we create an instance of class Transition whose constructor expects the name of the transition and an optional guard (true by default). A guard is specified as Expression('...') where '...' is an arbitrary Python expression, like Expression('x<5') in our example.

Arcs are added using one of the methods add_input or add_output of class PetriNet; both expect a place name, a transition name and the arc annotation as arguments (always in this order, place coming first). An input arc is directed from a place toward a transition, an output arc is outgoing a transition; so arcs are considered from the point of view of the transition to which they are connected. In particular, arc annotations may be:

• values as instances of class Value whose constructor simply expects the value that can be any Python object. For instances, Value(1) is the integer 1;
• variables names that can be bound to token values when a transition if executed. A variable is created by instantiating class Variable whose constructor expects the name of the variable as a Python string (matching regexp '[a-zA-Z]\w*');
• expressions to compute new values. An expression is an instance of class Expression whose constructor expects any Python expression as a string. In our example, Expression('x+1') as been used on the output arc.

The first step to execute a transition is to bind the variables labelling the input arcs to actual token values. This is possible by calling method modes() of a transition. It returns a list of Substitution instances that are dict-like objects to map variable names to values. Method modes returns a list of substitutions that enable the transition:

• each input arc, evaluated through the substitution, yields a multiset of tokens smaller than or equal to the current marking of the connected place;
• each output arc, evaluated through the substitution, yields a multiset of tokens that respects the type constraint of the connected place;
• the guard of the transition, evaluates to True through the substitution.

For instance, with our net, exactly one mode is available to fire the transition:

>>> n.transition('t').modes()
[Substitution(x=0)]

In order to fire a transition, we have to call its method fire with an enabling substitution as argument. In our example, we could run:

>>> n.transition('t').fire(Substitution(x=0))
>>> n.place('p').tokens
MultiSet([1])

Notice how attribute token allows to inspect the marking of each places. But we can also get the marking of a whole net:

>>> n.get_marking()
Marking({'p': MultiSet([1])})

Loading plugins

One of the most important feature of SNAKES is the plugin system that allows to extend any part of SNAKES. Let's see how plugins are loaded. In order to plug module snakes.plugins.foo into module snakes.nets, we have to use:

import snakes.plugins
snakes.plugins.load('foo', 'snakes.nets', 'my_nets')

Note that we have used just foo instead of snakes.plugins.foo because load will always search plugin modules from snakes.plugins. Intuitively, the (correct) statements above have the effect than the (incorrect) statement below:

import (snakes.nets + snakes.plugins.foo) as my_nets

So, after loading the plugin, we could load all of its content as we do for a regular Python module:

from my_nets import *

Several plugins may be loaded at the same time:

snakes.plugins.load(['foo', 'bar'], 'snakes.nets', 'my_nets')

This has the effect to load the plugin foo on the top of snakes.nets resulting in a module on the top of which bar is then loaded, which finally yields a module called my_nets.